Weekly Contest #48
(Ended)
Standings
Q1.
Let ![]() be the product of any three consecutive positive odd integers. The largest integer dividing all such
be the product of any three consecutive positive odd integers. The largest integer dividing all such ![]() is:?
is:?
Q2.
Let ![]() , where
, where ![]() is the smallest positive integer such that
is the smallest positive integer such that ![]() . Then the sum of the digits of
. Then the sum of the digits of ![]() is?
is?
Q3.
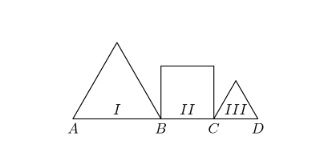
In this diagram, not drawn to scale, Figures ![]() and
and ![]() are equilateral triangular regions with respective areas of
are equilateral triangular regions with respective areas of ![]() and
and ![]() square inches. Figure
square inches. Figure ![]() is a square region with area
is a square region with area ![]() square inches. Let the length of segment
square inches. Let the length of segment ![]() be decreased by
be decreased by ![]() % of itself, while the lengths of
% of itself, while the lengths of ![]() and
and ![]() remain unchanged. The percent decrease in the area of the square is ?
remain unchanged. The percent decrease in the area of the square is ?
Q4.
With ![]() members voting the House of Representatives defeated a bill. A re-vote, with the same members voting, resulted in the passage of the bill by twice the margin by which it was originally defeated. The number voting for the bill on the revote was
members voting the House of Representatives defeated a bill. A re-vote, with the same members voting, resulted in the passage of the bill by twice the margin by which it was originally defeated. The number voting for the bill on the revote was ![]() of the number voting against it originally. How many more members voted for the bill the second time than voted for it the first time?
of the number voting against it originally. How many more members voted for the bill the second time than voted for it the first time?