Q1.

At a certain university, the division of mathematical sciences consists of the departments of mathematics, statistics, and computer science. There are two male and two female professors in each department. A committee of six professors is to contain three men and three women and must also contain two professors from each of the three departments. Find the number of possible committees that can be formed subject to these requirements.

Q2.

Ana, Bob, and Cao bike at constant rates of  meters per second,  meters per second, and  meters per second, respectively. They all begin biking at the same time from the northeast corner of a rectangular field whose longer side runs due west. Ana starts biking along the edge of the field, initially heading west, Bob starts biking along the edge of the field, initially heading south, and Cao bikes in a straight line across the field to a point  on the south edge of the field. Cao arrives at point  at the same time that Ana and Bob arrive at  for the first time. The ratio of the field's length to the field's width to the distance from point  to the southeast corner of the field can be represented as , where , , and  are positive integers with  and  relatively prime. Find .

Q3.

Find the number of positive integers  less than  for which there exists a positive real number  such that .

Note:  is the greatest integer less than or equal to .

Q4.

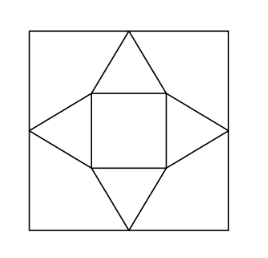
In the accompanying figure, the outer square  has side length . A second square  of side length  is constructed inside  with the same center as  and with sides parallel to those of . From each midpoint of a side of , segments are drawn to the two closest vertices of . The result is a four-pointed starlike figure inscribed in . The star figure is cut out and then folded to form a pyramid with base . Find the volume of this pyramid.